MD-Blog_Web Creative
算数ドリル ... 存在しない数?
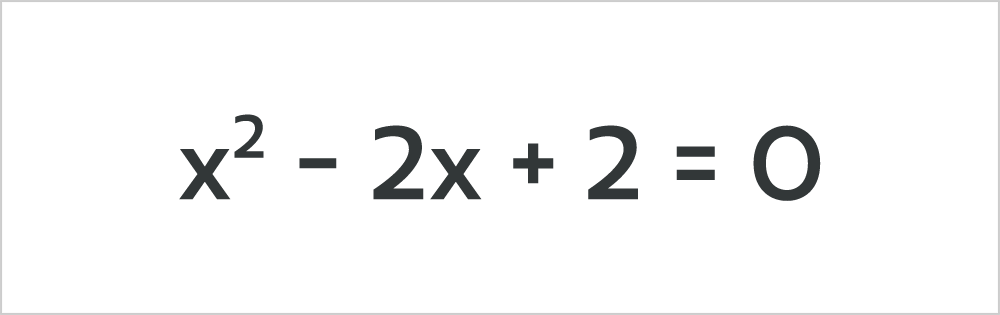
頭の体操
今年も師走になり、いかがバタバタとお過ごしでしょうか。(定型文)
年末ということで、今年のMONSTER DIVEのクリエイティブについて振り返らなくてもいいのか?という心の声?まわりからの声?も聞こえてくる気もするのですが、そこは初志貫徹ということで、少ないかもしれませんが、シリーズを期待してくれている人のために今年も「算数ドリル」シリーズをしましょう。
もう6年目5回目!
今回は二次方程式に関わる話なので、算数というより数学かもですがそこはご愛嬌ということで。
二次方程式の解
二次方程式を学ぶのは中学三年生ごろでしょうか。
そのころ「次の二次方程式を解きなさい。」で「解なし」という解答に誰も出会い、「解なし」って何だろう。「解なし」な式なんてあるのかと疑問に思ったと思います。
冒頭の画像の問題を実際に解くと下記のようになります。
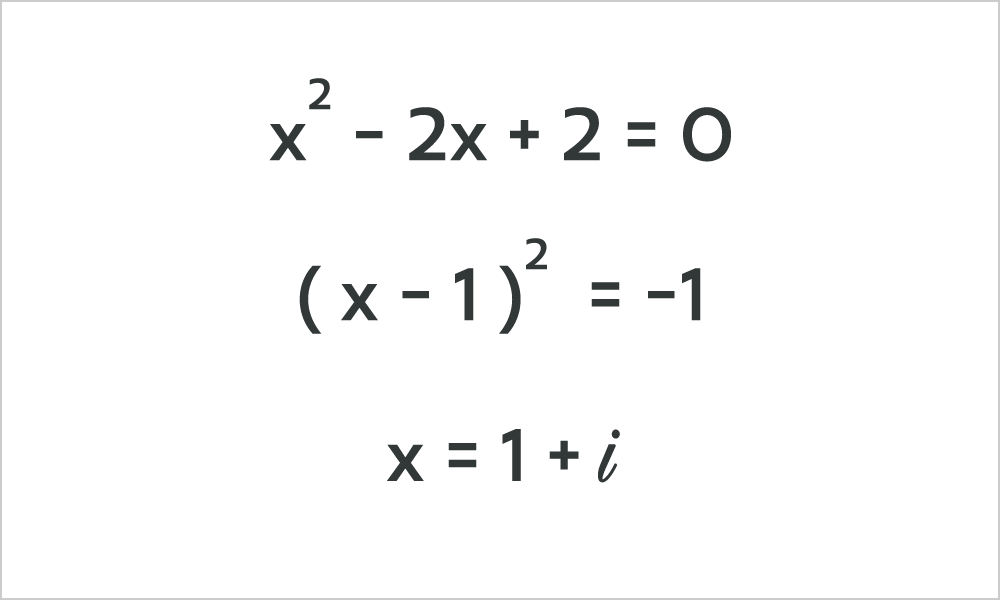
「解」がある!
ここからは高校数学な気もしますが、復習すると「i」を虚数。「1+i」を複素数と呼んでいました。
この虚数、複素数は現実には存在しない数なので、中学では「解なし」となっていたというわけです。
何故「i」を用いるかというと、実数は「real number」なので、それにあわせて「imaginary number」ということですね。
虚数、複素数
前段が長くなりましたが、何故このような思い出話?をしたのかというと、
「プログラミングの世界で虚数はどう表すのだろう?」
とふと疑問に思い、簡単にですが身近なプログラムを例にご紹介してみます。
ありますよね。そういうどうでもいいことが気になることって。
JavaScript
デフォルトではないが、math.js ライブラリを使用することで可能。
new Complex(re: number, im: number)
PHP
デフォルトではないが、PearのMath_Complexパッケージ で可能。
Math_Complex( float $real , float $im )
C
昔は複素数が使えなく、FORTRAN(懐かしい!)から抜け出せない人がいたようだが、今(C99以降)は「標準ライブラリー complex.h」で使える模様。
#include <complex.h> float _Complex x = 1.0 + 1.0 * _Complex_I ;
JAVA
こちらもデフォルトではないので、ApacheのComplexクラスで利用可能という話もありますが、自分で必要に応じて実装している人が多そう。
package org.apache.commons.math.complex;
public Complex(double real, double imaginary){ ... }
Python
complex型が標準で用意されている。素晴らしい!
# comp.real、comp.imag comp = 1 + j # comp = complex(re, im) comp = complex(1, 1)
※列挙したものより良いもの、「ここは!」、などあれば、ぜひツッコミしていただければです。
何に使う?
では実際に何に使うのでしょうか。
僕も今まで意識して使ったことはなかったのですが、オリジナルカオスやフラクタルの生成には必要でしょうし、実数部と虚数部にわかれることができるということは、1つの数で2つのベクトルが持てるということだと思うので、今までオブジェクトで管理していたものなどもすっきりスリムになったりと、使い道を考えるだけで楽しくなってきますね。
数字の世界が1次元から2次元へ広がったイメージ!?
一見複雑な処理や動きでも、実はこのような基本的な算数(数学)を使うと以外と簡単に制御できることも多いと思うので、ぜひ頭の体操がてらに使い道を考えてみるのも一興かと思います。
これぞ!という画期的な使い道が出てきたら僕にも教えてください。笑
算数ドリルシリーズ
- 算数ドリル ... 動的レイアウトを考えよう
- 算数ドリル ... 三角関数sin/cosの基本
- 算数ドリル ... 2点間の距離と角度
- 算数ドリル ... ビット演算で買い忘れを防ごう
- 算数ドリル ... 存在しない数?
- Recent Entries
-
- 誰でも簡単に使えるポン出しアプリ(サンプラー) 「Klang2」をご紹介!【Part2】
- 画像を読み込ませるだけでコードを書かずにWebサイトを作れる「Windsurf」を試してみた
- 高額療養費制度を実際に利用してみた! 申請から給付までの流れ
- ライブ配信の仕事って実際どうなの? 現場のリアルを担当者が語る!職種別インタビュー!
- 実践に役立つ【ペルソナ設計】のポイントを、 WEBディレクターが真剣に考えてみました!
- ハイエースドライバーへの道 vol.2 〜免許取得から数ヶ月...ハイエース運転で味わった苦い経験と、社内で動き出した「運転手」のためのルールづくり〜
- 気づけば5年目!未経験ディレクターがここまで来た話
- アイディアを実現させる、MONSTER DIVEが創るライブ配信
- 大規模イベントで活躍中!Solidcom C1 Pro - Roaming Hub
- アルムナイ採用された側は、戻ってきた会社に何を感じたか
- MD EVENT REPORT
-
- MDの新年はここから。毎年恒例の新年のご祈祷と集合写真
- 2024年もMONSTER DIVE社内勉強会を大公開!
- 社員旅行の計画は「コンセプト」と「事前準備」が重要! 幹事さん必見! MONSTER DIVEの社内イベント事例
- 5年ぶりの開催! MONSTER DIVE社員旅行2024 "Build Our Team"!
- よいモノづくりは、よい仲間づくりから 「チームアクティビティ支援制度」2023年活動報告!
- 2023年のMONSTER DIVE勉強会を大公開!
- リフレッシュ休暇の過ごし方
- 勤続10周年リフレッシュ25連休で、思考をコンマリしたりタイに行った話。
- 俺たちのフジロック2022(初心者だらけの富士山登山)
- よいモノづくりは、コミュニケーションから始まる
- What's Hot?
-
- 柔軟に対応できるフロントエンド開発環境を構築する 2022
- 楽しくチームビルディング! 職場でおすすめのボードゲームを厳選紹介
- ライブ配信の現場で大活躍! 「プロンプター」とは?
- 名作ゲームに学べ! 伝わるUI/UXデザインのススメ
- 映像/動画ビギナーに捧げる。画面サイズの基本と名称。
- [2020最新版] Retinaでもボケない、綺麗なfaviconの作り方
- ビット(bit), バイト(Byte), パケット。ついでにbps。 〜後編「で、ビットとバイトって何が違うの?」〜
- 有名企業やブランドロゴに使われているフォントについて調べてみる。
- 算数ドリル ... 2点間の距離と角度
- 画面フロー/システムフローを考えよう!
- タグリスト
-
- #Webデザイン
- #JavaScript
- #MONSTER DIVE
- #映像制作
- #Movable Type
- #ライブ配信
- #CMS
- #ワークスタイル
- #MONSTER STUDIO
- #Webプロモーション
- #Web開発
- #アプリ
- #Creators Lab まとめ
- #Webディレクターのノウハウ
- #MTタグを極める
- #効率化
- #MD社内イベント
- #CSS
- #撮影
- #プランニング
- #Webクリエイティブ
- #オーサリング
- #クレバー藤原
- #コーディング
- #スマートフォン
- #Webディレクション
- #早朝がいちばん捗るヒト
- #PowerCMS
- #グラフィックデザイン
- #ストリーミング配信
- #WEBサービス
- #サマンサ先生
- #人事
- #Android
- #iPhone
- #Webメディア
- #まとめ
- #ディレクション
- #プログラミング
- #新入社員
- #HTML5
- #iOS
- #jquery
- #RIDE HI
- #UI/UXデザイン
- #プラグイン
- #ライブ中継
- #Adobe
- #アニメーション
- #プロジェクト管理
